ColMap学习

Spade-Atek2025/03/04SoftwareColMap

COLMAP源码解读+实践

  base/ —— 基础数据结构（相机、图像、关键点、匹配等）
  feature/ —— 关键点检测与特征匹配
  sfm/ —— 结构化运动（SFM）模块，包含增量式和全局式 SFM
  mvs/ —— 稠密重建（MVS）模块，包含深度估计和点云融合
  optim/ —— 主要用于优化（如 BA 束调整）
  util/ —— 实用工具（日志、并行计算等）

1. 特征提取与匹配（feature/）

提取 SIFT 关键点（是一些十分突出的不会因光照、尺度、旋转等因素而消失的点)，并进行匹配

// 在增量 SFM 之前，COLMAP 需要先从图像中提取特征点并进行匹配。COLMAP 默认使用 SIFT（尺度不变特征变换） 进行特征提取：
void SiftGPUFeatureExtractor::ExtractFeatures() {
    SiftGPU sift;
    sift.RunSIFT();
}

用大模型构建了SIFT的代码，下面是效果 alt text 两张图片匹配 alt textalt text

2. 增量式 SfM（sfm/）：构建稀疏点云，包括相机位姿估计、三角化、BA

2.1 初始化（Initial Pair Selection）

选择一个合适的图像对作为初始的两张图片
计算基础矩阵 (Essential Matrix, E) 进行姿态估计
三角化计算 3D 点云

2.2 增量扩展（Incremental Mapping）

选取下一张照片，利用已有 3D 点云进行位姿估计
进行新点的三角化，并进行 BA（束调整）
逐步加入更多照片

2.3 全局优化

进行完整的 BA（全局优化相机位姿、3D 点）
处理漂移问题

3. 稠密重建（mvs/）：估算深度图并融合点云，生成稠密模型

SFM 计算出相机位姿后，COLMAP 进入 MVS（多视角立体匹配） 阶段。代码位于 src/mvs/ 目录下。 MVS 的核心流程如下：

1. 计算深度图（PatchMatch Stereo）
2. 深度融合（Depth Map Fusion）
3. 生成稠密点云.

COLMAP 采用 PatchMatch Stereo 进行深度估计，该算法通过 滑动窗口匹配 计算像素深度，并采用 代价聚合 + 视图一致性检查 来优化深度图。

4. COLMAP文件结构

+── images  # images文件夹包含未失真的图像
│   +── image1.jpg
│   +── image2.jpg
│   +── ...
+── sparse  # sparse文件夹包含使用未失真相机进行的稀疏重建
│   +── cameras.txt
│   +── images.txt
│   +── points3D.txt
+── stereo  # stereo文件夹包含立体重建结果
│   +── consistency_graphs
│   │   +── image1.jpg.photometric.bin
│   │   +── image2.jpg.photometric.bin
│   │   +── ...
│   +── depth_maps
│   │   +── image1.jpg.photometric.bin
│   │   +── image2.jpg.photometric.bin
│   │   +── ...
│   +── normal_maps
│   │   +── image1.jpg.photometric.bin
│   │   +── image2.jpg.photometric.bin
│   │   +── ...
│   +── patch-match.cfg
│   +── fusion.cfg
+── fused.ply
+── meshed-poisson.ply
+── meshed-delaunay.ply
+── run-colmap-geometric.sh
+── run-colmap-photometric.sh

包含相机、图像和points3D文件的文件夹 COLMAP 为每个重建模型导出以下三个文本文件： cameras.txt、images.txt和points3D.txt

cameras.txt 该文件包含数据集中所有重建相机的固有参数，每个相机一行，例如：

# Camera list with one line of data per camera:
#   CAMERA_ID, MODEL, WIDTH, HEIGHT, PARAMS[]
# Number of cameras: 3
1 SIMPLE_PINHOLE 3072 2304 2559.81 1536 1152
2 PINHOLE 3072 2304 2560.56 2560.56 1536 1152
3 SIMPLE_RADIAL 3072 2304 2559.69 1536 1152 -0.0218531

此处，数据集包含 3 个基于不同失真模型的相机，它们具有相同的传感器尺寸（宽度：3072，高度：2304）。参数的长度是可变的，取决于相机型号。对于第一台相机，有 3 个参数，单个焦距为 2559.81 像素，主点位于像素位置(1536, 1152)。相机的固有参数可以由多幅图像共享，这些图像使用唯一标识符CAMERA_ID来引用相机。

images.txt 该文件包含数据集中所有重建图像的姿势和关键点，每个图像两行，例如：

# Image list with two lines of data per image:
#   IMAGE_ID, QW, QX, QY, QZ, TX, TY, TZ, CAMERA_ID, NAME
#   POINTS2D[] as (X, Y, POINT3D_ID)
# Number of images: 2, mean observations per image: 2
1 0.851773 0.0165051 0.503764 -0.142941 -0.737434 1.02973 3.74354 1 P1180141.JPG 2362.39 248.498 58396 1784.7 268.254 59027 1784.7 268.254 -1
2 0.851773 0.0165051 0.503764 -0.142941 -0.737434 1.02973 3.74354 1 P1180142.JPG 1190.83 663.957 23056 1258.77 640.354 59070

这里，前两行定义了第一幅图像的信息，依此类推。图像的重建姿态被指定为使用四元数(QW, QX, QY, QZ) 和平移向量(TX, TY, TZ)从世界到图像的相机坐标系的投影。四元数使用汉密尔顿约定定义，例如，Eigen 库也使用该约定。投影/相机中心的坐标由 给出，其中 是由四元数组成的 3x3 旋转矩阵的逆/转置，是平移向量。图像的局部相机坐标系的定义方式是，从图像来看，X 轴指向右侧，Y 轴指向下方，Z 轴指向前方。-R^t * TR^tT 上例中的两幅图像使用相同的相机型号并共享内在函数 ( CAMERA_ID = 1 )。图像名称与项目选定的基础图像文件夹相关。第一幅图像有 3 个关键点，第二幅图像有 2 个关键点，而关键点的位置以像素坐标指定。两幅图像都观察到 2 个 3D 点，请注意，第一幅图像的最后一个关键点在重建中没有观察到 3D 点，因为 3D 点标识符为 -1。

points3D.txt 该文件包含数据集中所有重建的 3D 点的信息，每个点一行，例如：

# 3D point list with one line of data per point:
#   POINT3D_ID, X, Y, Z, R, G, B, ERROR, TRACK[] as (IMAGE_ID, POINT2D_IDX)
# Number of points: 3, mean track length: 3.3334
63390 1.67241 0.292931 0.609726 115 121 122 1.33927 16 6542 15 7345 6 6714 14 7227
63376 2.01848 0.108877 -0.0260841 102 209 250 1.73449 16 6519 15 7322 14 7212 8 3991
63371 1.71102 0.28566 0.53475 245 251 249 0.612829 118 4140 117 4473

这里有三个重建的 3D 点，其中POINT2D_IDX定义images.txt文件中关键点的从零开始的索引。误差以重新投影误差的像素为单位给出，并且仅在全局光束调整后更新。 colmap的特征提取，内置是SIFT特征，如果要使用现有特征，可以从文本文件中导入现有特征，每个图像旁边都必须有一个文本文件（例如， /path/to/image1.jpg和/path/to/image1.jpg.txt）并有规定的格式

PyCOLMAP PyCOLMAP 向 Python 公开了 COLMAP 的大部分功能。

对极几何

目的：特征匹配（相似度）——高不一定是匹配上了——对极几何，减少匹配范围，提高匹配精度。 基线baseline、极点唯一，极线、极平面在一幅影像里面不唯一 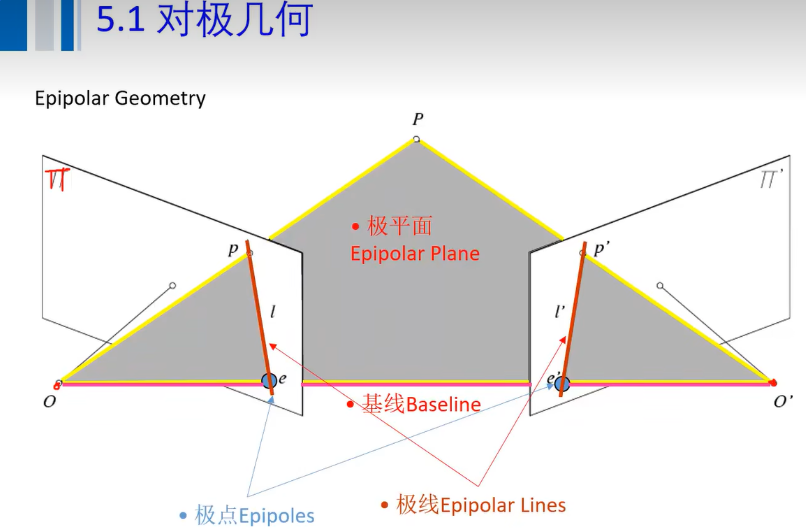alt text 基础矩阵 本质矩阵 单应矩阵

Edit this page
ON THIS PAGE